chapter 9 Co-ordinate Geometry

发表于 2025-01-05 分类于 an introduction to mathematics

CO-ORDINATE GEOMETRY

THE METHODS and ideas of co-ordinate geometry have already been employed in the previous chapters. It is now time for us to consider them more closely for their own sake; and in doing so we shall strengthen our hold on other ideas to which we have attained. In the present and succeeding chapters we will go back to the idea of the positive and negative real numbers and will ignore the imaginaries which were introduced in the last two chapters.

坐标几何的方法和思想已经在前几章中得到应用。现在是时候为了其本身的意义更仔细地考虑它们了；这样做时，我们将加深对我们已经掌握的其他思想的理解。在本章和接下来的章节中，我们将回到正负实数的概念，忽略在过去两章中引入的虚数。

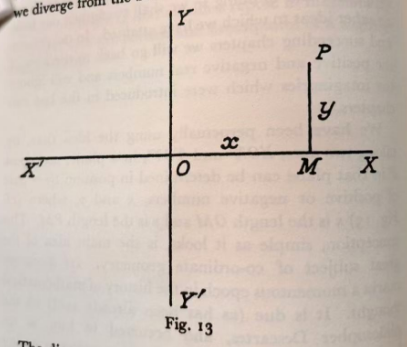
We have been perpetually using the idea that, by taking two axes, XOX' and YOY', in a plane, any point P in that plane can be determined in position by a pair of positive or negative numbers, x and y, where (cf.Fig.13) x is the length OM and y is the length PM. This conception, simple as it looks, is the main idea of the great subject of co-ordinate geometry. Its discovery makes a momentous epoch in the history of mathematical thought. It is due (as has been already said) to the philosopher Descartes, and occurred to him as an important mathematical method one morning as he lay in bed. Philosophers, when they have possessed a thorough knowledge of mathematics, have been among those who have enriched the science with some of its best ideas. On the other hand, it must be said that, with hardly an exception, all the remarks on mathematics made by those philosophers who have possessed but a slight or hasty and late-acquired knowledge of it are entirely worthless, being either trivial or wrong. The fact is a curious one; since the ultimate ideas of mathematics seen, after all, to be very simple, almost childishly so, and to lie well within the province of philosophical thought. Probably their very simplicity is the cause of error; we are not used to think about such simple abstract things, and a long training is necessary to secure even a parital immunity from error as soon as we diverge from the beaten track of thought.

我们一直在持续使用这样一个概念：通过在平面上取两个坐标轴 XOX' 和 YOY'，平面上的任何一点 P 都可以通过一对正数或负数（x 和 y）来确定其位置，其中（参见图13）x 是 OM 的长度，y 是 PM 的长度。这个看似简单的概念是坐标几何这个伟大学科的核心思想。它的发现标志着数学思想史上的一个重要转折点。正如之前所说，这一发现归功于哲学家笛卡尔，并且是在某个早晨，他躺在床上时偶然想到的一个重要的数学方法。当哲学家们掌握了深厚的数学知识时，他们便成了那些为数学科学贡献了其中一些最佳思想的人之一。另一方面，不得不说，几乎没有例外，所有那些仅有少量、匆忙和后天获得的数学知识的哲学家所做的关于数学的评论都是完全没有价值的，要么是琐碎的，要么是错误的。这个事实本身很有趣；因为数学的最终思想实际上是非常简单的，几乎可以说是孩子气的，而且它完全属于哲学思维的范畴。或许正是它们的简洁性导致了错误的产生；我们不习惯思考如此简单的抽象事物，并且需要经过长时间的训练才能在偏离传统思维轨道时，至少部分免于犯错。

The discovery of co-ordinate geometry, and also that of projective geometry about the same time, illustrate another fact which is being continually verified in the history of knowledge, namely, that some off the greatest discoveries are to be made among the most well-know topics. By the time that the seventeenth century had arrived, geometry had already been studied for over two thousand years, even if we date its rise with the Greeks. Euclid taught in the University of Alexandria, being born about 330 B.C.; and he only systematized and extended the work of a long series of predecessors, some of them men of genius. After him generation after generation mathematicians laboured at the improvement of the subject. Nor did the subject suffer from that fatal bar to progress, namely, that its study was confined to a narrow group of men of similar origin and outlook—quite the contrary was the case ; by the seventeenth century it had passed through the minds of Egyptians and Greeks, of Arabs and of Germans. And yet, after all this labour devoted to it through so many ages by such diverse minds its most important secrets were yet to be discovered.

坐标几何的发现，以及大约在同一时期投影几何的发现，说明了一个在知识史中不断得到验证的事实，即一些最伟大的发现往往是在最为人熟知的领域中产生的。到了十七世纪时，几何学已经被研究了两千多年，即使我们将它的兴起追溯到古希腊。欧几里得大约在公元前330年出生，他在亚历山大里亚大学讲学；他只是将一系列前人的工作进行了系统化和扩展，其中一些前人是天才人物。此后，一代又一代的数学家们致力于这门学科的改进。学科并没有遭遇那种致命的进步障碍——即研究仅限于一个背景和观点相似的狭小群体，恰恰相反，情况并非如此；到了十七世纪，几何学已经穿越了埃及人、希腊人、阿拉伯人和德国人的思想。而尽管经过如此多代不同思想者的辛勤耕耘，几何学最重要的秘密仍然没有被发现。

No one can have studied even the elements of elementary geometry without feeling the lack of some guiding method. Every proposition has to be proved by a fresh display of ingenuity; and a science for which this is true lacks the great requisite of scientific thought, namely, method. Now the especial point of co-ordinate geometry is that for the first time it introduced method. The remote deductions of a mathematical science are not of primary theoretical importance. The science has not been perfected, until it consists in essence of the exhibition of great allied methods by which information, on any desired topic which falls within its scope, can easily be obtained. The growth of a science is not primarily in bulk, but in ideas; and the more the ideas grow, the fewer are the deductions which it is worth while to write down. Unfortunately, mathematics is always encumbered by the repetition in text-books of numberless subsidiary prepositions, whose importance has been lost by their absorption into the role of particular cases of more general truths—and, as we have already insisted, generality is the soul of mathematics.

没有人能够仅仅学习几何学的基本要素而不感受到缺乏某种指导方法的困惑。每一个命题都需要通过全新的创造性表现来加以证明；而对于一门科学，如果这种情况属实，那么它就缺乏科学思想的最重要条件——也就是方法。而坐标几何的特殊意义在于，它首次引入了方法。数学科学中那些抽象而深远的推论并非理论上的首要重要事项。一门科学还未臻于完善，除非它的本质在于展示一系列伟大的相关方法，通过这些方法，可以轻松获得任何属于其研究范围内主题的信息。科学的发展主要体现在思想上，而不是体现在规模上；而且，思想越深入发展，值得记录下来的推导就越少。遗憾的是，数学总是被教科书中无数次重复的次要命题所拖累。这些命题的重要性因其被归入更一般真理的特殊情况而丧失——正如我们已经强调过的那样，一般性是数学的灵魂。

Again, co-ordinate geometry illustrates another feature of mathematics which has already been pointed out, namely, that mathematical sciences as they develop dovetail into each other, and share the same ideas in common. It is not too much to say that the various branches of mathematics undergo a perpetual process of generalization, and that as they become generalized, they coalesce. Here again the reason springs from the very nature of the science, its generality, that is to say, from the fact that the science deals with the general truths which apply to all things in virtue of their very existence as things. In this connexion the interest of co-ordinate geometry lies in the fact that it relates together geometry, which started as the science of space, and algebra, which has its origin in the science of number.

再次，解析几何展现了数学的另一个特性，这一特性此前已经被提到过：数学科学在其发展过程中彼此衔接，并共享相同的思想内容。可以毫不夸张地说，数学的各个分支经历着一个永恒的普遍化过程，而随着它们的普遍化，它们逐渐融合在一起。这里再次强调，这种现象的原因源于科学本身的本质——它的普遍性。换句话说，这种原因源于科学研究的是适用于一切事物的普遍真理，而这些真理是基于事物本身作为存在之物的特性。在这一背景下，解析几何的意义在于它将几何学和代数学联系在了一起：几何学最初是空间的科学，而代数学起源于数的科学

Let us now recall the main ideas of the two sciences, and then see how they are related by Descartes's method of co-ordinates. Take algebra in the first place. We will not trouble ourselves about the imaginaries and will think merely of the real numbers with positive or negative signs. The fundamental idea id that of any number, the variable number, which is denoted by a letter and not by any definite numberal. We then proceed to the consideration of correlations between variables. For example, fi x and y are two variables, we may conceive them as correlated by the equations , or by , or in any one of an indefinite number of other way. That at once leads to the application of the idea of algebraic form. We think, in fact, of any correlation of some interesting type, thus rising from the initial conception of variable numbers to the secondary conception of variable correlations of numbers. Thus we generalize the correlation , into correlation . Here and and , being letters, stand for any numbers and are in fact themselves variables. But they are the variables which determine the variables correlation; and the correlation, when determined, correlate the variable numbers and . Variables, like , , and above, which are used to determine the correlation are called 'constant' , or parameters. The use of the term 'constant' in this connextion for what is really a variable may seem at first sight to be odd; but it is really very natural. For the mathematical investigation is concerned with the relation between the variables and , after ,, are supposed to have been determined. So in a sense, relatively to and , the 'constant' , , and are constants. Thus stands for the general example of a certain algebraic form, that is, for a variable correlation belonging to a certain class.

现在让我们回顾一下这两门科学的主要思想，然后看看它们是如何通过笛卡尔的坐标法则相关联的。首先考虑代数。我们不去关注虚数，而仅仅考虑带有正负符号的实数。基本的思想是任何数的概念，即变量数，这个数用字母表示，而不是任何具体的数字。接下来，我们开始考虑变量之间的相关性。例如，如果和是两个变量，我们可以把它们看作是通过方程或或通过其他无限多种方式相关联的。这立即引出了代数形式的应用。事实上，我们会考虑某种有趣类型的相关性，从而从最初的变量数的概念过渡到变量之间相关性的次级概念。因此，我们将相关性一般化为相关性。这里，、和是字母，代表任何数，实际上它们本身也是变量。但它们是决定变量相关性的变量；而当相关性被确定时，它们就关联了变量和。像上面的、和这样的变量，被用来确定相关性，称为“常数”或参数。在这种情况下，使用“常数”一词来表示实际上是变量的东西，乍一看似乎有些奇怪；但实际上这是很自然的。因为数学研究关注的是在假定、和已经被确定之后，和之间的关系。因此，从相对和的角度来看，“常数” 、和确实是常数。因此，方程代表了某种代数形式的一般例子，也就是说，代表了一类变量相关性的例子。

Again we generalize in to , or still further in to , or , still further, into . Here again we are led to variable correlations which are indicated by their various algebraic forms.

我们再次将一般化为，或者进一步一般化为，甚至进一步一般化为。在这里，我们再次得到了通过它们各自的代数形式表示的变量相关性。

Now let us turn to geometry. The name of the science at once recalls to our minds the thought of figures and diagrams exhibiting triangles and rectangles and squares and circles, all in special relations to each other. The study of the simple properties of these figures is the subject matter of elementary, as it is rightly presented to the beginner. Yet a moment's thought will show that this is not the true conception of the subject. It may be right for a child to commence his geometrical reasoning on shapes, like triangles and squares, which he has cut out with scissors. What, however, is a triangles? It is a figure marked out and bounded by three bits of three straight lines.

现在让我们转向几何学。这个学科的名字立刻使我们联想到图形和图表，展示了三角形、矩形、正方形和圆形，它们彼此之间有着特殊的关系。这些图形的简单性质研究是初学者学习几何时所接触的内容。然而，稍作思考就会发现，这并不是该学科的真正概念。对一个孩子来说，开始几何推理时，研究他用剪刀剪出的三角形和正方形是合适的。然而，三角形到底是什么呢？它是由三条直线段所标出并界定的图形。

Now the boundary of spaces by bits of lines is a very complicated idea, and not at all one which gives any hope of exhibiting the simple general conceptions which should form the bones of the subject. We want something more simple and more general. It is this obsession with the wrong initial ideas—very natural and good ideas for the creation of first thoughts on the subject—which was the cause of the comparative sterility[ stəˈrɪləti ] of the study of the science during so many centuries. Co-ordinate geometry, and Descartes its inventor, must have the credit of disclosing the true simple objects for geometrical thought.

现在，使用直线段界定空间的边界是一个非常复杂的概念，根本不能为展示应构成该学科基本框架的简单一般性概念提供任何希望。我们需要更简单、更一般的东西。正是对错误初步概念的执着——这些概念对该学科初步思考的形成来说是非常自然和有效的——导致了该学科在许多个世纪里的相对贫瘠。坐标几何，以及其发明者笛卡尔，必须因揭示几何思维的真正简单对象而获得应有的功勋。

In the place of a bit of a straight line, let us think of the whole of a straight line throughout its unending length in both directions. This is the sort of general idea from which to start our geometrical investigation. The Greeks never seem to have found any use for this conception which is now fundamental in all modern geometrical thought. Euclid always contemplates a straight line as drawn between two definite points, and is very careful to mention when it is to be produced beyond this segment. He never thinks of the line as an entity given once for all as a whole. This careful definition and limitation, so as to exclude an infinity not immediately apparent to the senses, was very characteristic of the Greeks in all their many activities. It is enshrined in the difference between Greek architecture and Gothic architecture, and between the Greek religion and the modern religion. The spire on a Gothic cathedral and the importance of the unbounded straight line in modern geometry are both emblematic of the transformation of the modern world.

在一条直线的一小段位置上，让我们考虑一条直线的整个长度，向两端延伸且没有尽头。这就是我们开始几何学研究的那种一般性概念。古希腊人似乎从未发现过这种如今在所有现代几何思想中都至关重要的概念。欧几里得总是将直线看作是从两个确定的点之间画出的，并且非常小心地提到何时需要将其延伸超出这个段落。他从不把直线看作是一次性确定的整体实体。这种精确的定义和限制，旨在排除一个感官上无法立即察觉到的无限，正是古希腊人在其所有许多活动中的典型特征。它被珍藏在希腊建筑与哥特建筑之间的差异中，以及希腊宗教与现代宗教之间的区别中。哥特大教堂的尖塔和现代几何学中无界直线的重要性，都是现代世界转型的象征。

The straight line, considered as a whole, is accordingly the root idea from which modern geometry starts. But then other sorts of lines occur to us, and we arrive at the conception of the complete curve, which at every point of it exhibits some uniform characteristic, just as the straight line exhibits at all points the characteristic of straightness. For example, there is the circle which at all point exhibits the characteristic of being at a given distance form its centre, and again there is the ellipse, which is an oval curve, such that the sum of the two distances of any point on it from two fixed points, called its foci, is constant for all points on the curve. It is evident that a circle is merely a particular case of an ellipse when the two foci are superposed in the same point; for then the sum of the two distances is merely twice the radius of the circle. The ancients knew the properties of the ellipse and the circle and, of course, considered them as wholes. For example, Euclid never starts with mere segments (i.e. bits) of circles, which are then prolonged. He always considers the whole circle as described. It is unfortunate that the circle is not the true fundamental line in geometry, so that his defective consideration of the straight line might have been of less consequence.

因此，直线作为一个整体，可以说是现代几何学的根本概念。然后，其他种类的线条也出现在我们的思维中，我们于是得出了完整曲线的概念，它在每个点上都展示某种统一的特征，就像直线在所有点上展示直线性的特征一样。例如，圆形在每个点上都表现出与其中心保持固定距离的特征，再如椭圆，它是一种椭圆曲线，任何一点到两个固定点（称为焦点）的距离之和，对于曲线上的所有点都是恒定的。显然，圆形仅仅是椭圆的一种特例，当两个焦点重合于同一点时；因为在这种情况下，两个距离的和恰好是圆的直径。古人知道椭圆和圆形的性质，当然也将它们视为整体。例如，欧几里得从不从圆的单独弧段（即部分）开始，然后将其延长。他总是将整个圆作为已描绘的图形来考虑。遗憾的是，圆形并不是几何学中的真正基础线，因此他对直线的缺陷性考虑可能影响较小。

This general idea of a curve which at any point of it exhibits some uniform property is expressed in geometry by the term 'locus'. A locus is the curve (or surface, if we do not confine ourselves to a plane) formed by points, all of which possess some given property. To every property in relation to each other which points can have, there corresponds some locus, which consists of all the points possessing the property. In investigating the properties of a locus considered as a whole, we consider point or points on the locus. Thus in geometry we again meet with the fundamental idea of the variable. Furthermore, in classifying loci under such headings as straight lines, circles, ellipses, &c., we again find the idea of form.

在几何学中，任何一点上都表现出某种统一性质的曲线的这一一般概念，用术语“轨迹”来表示。轨迹是由所有具有某一给定性质的点所形成的曲线（或曲面，如果我们不局限于平面的话）。对于点之间可以具有的每一种性质，都对应着某个轨迹，这个轨迹由所有具有该性质的点组成。在研究作为整体的轨迹的性质时，我们考虑轨迹上的任何一点或多个点。因此，在几何学中，我们再次遇到了变量这一基本概念。此外，在将轨迹分类为直线、圆、椭圆等类别时，我们再次发现了形式的概念。

Accordingly, as in algebra we are concerned with variable numbers, correlations between variable numbers, and the classification of correlations into types by the idea of algebraic form; so in geometry we are concerned with variable points, variable points satisfying some conditions so as to form a locus, and the classification of loci into types by the idea of conditions of the same form.

因此，正如在代数中我们关注变量数字、变量数字之间的关联以及根据代数形式的理念将这些关联分类成不同类型；在几何中，我们关注变量点，满足某些条件以形成轨迹的变量点，以及根据相同形式的条件将轨迹分类成不同类型。

Now, the essence of co-ordinate geometry is the identification of the algebraic correlation with the geometrical locus. The point on a plane is represented in algebra by its two co-ordinates, and , and the condition satisfied by any point on the locus is represented by the corresponding correlation between and . Finally to correlations expressible in some general algebraic form, such as , there correspond loci of some general type, whose geometrical conditions are all of the same form. We have thus arrived at a position where we can effect a complete interchange in ideas and results between the two sciences. Each science throws light on the other, and itself gains immeasurably in power. It is impossible not to feel stirred at the thought of the emotions of men at certain historic moments of adventure and discovery—Columbus when he first saw the Western shore, Pizarro when he started at the Pacific Ocean, Franklin when the electric spark came from the string of his kite, Galileo when he first turned his telescope to the heavens. Such moments are also granted to students in the abstract regions of thought, and high among them must be placed the morning the Descartes lay in bed and invented the method of co-ordinate geometry.

现在，坐标几何的本质在于将代数相关性与几何轨迹进行识别。平面上的点通过其两个坐标和在代数中表示，任何位于轨迹上的点所满足的条件则通过和之间的相应相关性来表示。最后，对于可以用某种一般代数形式表示的相关性，例如，则对应某种一般类型的轨迹，其几何条件均为相同的形式。通过这种方式，我们已经达到了一个可以在这两门科学之间实现完全思想和结果互换的地步。每一门科学都能为另一门科学提供启发，且其自身的力量也得到了极大的增强。想到人们在某些历史冒险与发现的时刻所激发的情感，真是令人激动——哥伦布首次看到西方海岸时，皮萨罗启程面向太平洋时，富兰克林从风筝线中看到电火花时，伽利略第一次将望远镜对准天空时。这样的时刻也赋予了抽象思维领域的学者们，在这些时刻中，最值得纪念的便是笛卡尔躺在床上，发明了坐标几何的方法的那一天。

When one has once grasped the idea of co-ordinate geometry, the immediate question which starts to the mind is , What sort of loci correspond to the well know algebraic form? For example, the simplest among the general types of algebraic forms is . The sort of locus which corresponds to this is a straight line, and conversely to every straight line there corresponds an equation of this form. It is fortunate that the simplest among the geometrical loci should correspond to the simplest among the algebraic forms. Indeed, it is this general correspondence of geometrical and algebraic simplicity which gives to the whole subject its power. It springs form the fact that the connextion between geometry and algebra is not casual and artificial, but deep-seated and essential. The equation which corresponds to a locus is called the equation 'of' (or 'to') the locus. Some examples of equations of straight lines will illustrate the subject.

当一个人一旦掌握了坐标几何的概念，紧接着产生的第一个问题是：什么样的轨迹与著名的代数形式相对应？例如，代数形式中的最简单类型是。与这个代数形式对应的轨迹是直线，反过来，每一条直线都对应一个这样的方程。幸运的是，几何轨迹中最简单的与代数形式中最简单的相对应。事实上，正是几何和代数的这种普遍对应性，赋予了整个学科其力量。它源于几何与代数之间的联系不是偶然和人为的，而是深刻且本质的。与轨迹相对应的方程被称为轨迹的方程（或“与轨迹对应的方程”）。一些直线方程的例子将有助于阐明这个主题。

Consider ; here the and , of the general form have been replace by , and respectively. This line passes through the 'origin', , in the diagram and bisects the angle . It is the line of the diagram. The fact that it passes through the origin, , is easily seen by observing that the equation is satisfied by putting and simultaneously, but and are the co-ordinates of . In fact it is easy to generalize and to see by the same method that the equation of any line through the origin is of the form . The locus of equation also passes through the origin and bisects the angle : it is the line of the diagram.

考虑方程；这里，一般形式中的、和分别被替换为、和。这条直线通过图中的原点，并平分角。它就是图中的直线。这条直线通过原点，这一点很容易看出来，因为将和同时代入方程，方程成立，而和正是原点的坐标。事实上，通过相同的方法，我们很容易推广并看出，任何经过原点的直线的方程都可以表示为。方程的轨迹同样通过原点，并平分角；它就是图中的直线。

Consider : the corresponding locus does not pass through the origin. We therefore seek where it cuts the axes. It must cut the axis of x at some point of co-ordinates and . But putting in the equation, we get ; so the co-ordinates of the point () are and . Similarly the point () where the line cuts the axis are and . The locus is the line in the figure and is parallel to . Similarly is the equation of line of the figure; and the locus is parallel to . It is easy to prove the general theorem that two lines represented by equations of the forms and are parallel.

考虑方程：对应的轨迹不通过原点。因此，我们要寻找它与坐标轴的交点。它必定在 x 轴上与某一点相交，该点的坐标是和。将代入方程，我们得到；所以该点 () 的坐标是和。类似地，直线与轴的交点 () 的坐标是和。该轨迹是图中的直线，并且与直线平行。类似地，方程是图中直线的方程；该轨迹与直线平行。通过类似的方法，容易证明一般定理：由方程形式为和表示的两条直线是平行的。

The group of loci which we next come upon are sufficiently important to deserve a chapter to themselves. But before going on to them we will dwell a little longer on the main ideas of the subject.

我们接下来要讨论的轨迹组足够重要，值得单独成章。但在继续讨论它们之前，我们将稍微再深入一下这个主题的主要思想。

The position of any point is determined by arbitrarily choosing an origin, , two axes, and , at right-angles, and then by nothing its coordinates and , i.e. and (cf. Fig. 13). Also , as we have seen in the last chapter, can be determined by the 'vector' , the the idea of the vector includes a determinate direction as well as a determinate length. From an abstract mathematical point of view the idea of an arbitrary origin may appear artificial and clumsy, and similarly for the arbitrarily drawn axes, and . But in relation to the application of mathematics to the event of the Universe we are here symbolizing with direct simplicity the most fundamental fact respecting the outlook on the world afforded to us by our senses. We each of us refer our sensible perceptions of things to an origin which we call 'here': our location in a particular part of space round which we group the whole Universe is the essential fact of our bodily existence. We can imagine beings who observe all phenomena in all space with an equal eye, unbiased in favour of any part. With us it is otherwise, a cat at our feet claims more attention than an earthquake at Cape Horn, or than the destruction of a world in the Milky Way. It is true that in making a common stock of our knowledge with our fellowmen, we have to waive something of the strict egoism of our own individual 'here'. We substitute 'nearly here' for 'here'; thus we measure miles from the town hall of the nearest town, or from the capital of the country. In measuring the earth, men of science will put the origin at the earth's centre; astronomers even rise to the extreme altruism of putting their origin inside the sun. But, far as this last origin may be, and even if we go further to some convenient point amid the nearer fixed stars,yet, compared to the immeasurable infinities of space, it remains true that our first procedure in exploring the Universe is to fix upon an origin 'near here'.

任何点的位置是通过任意选择一个原点、两个互相垂直的坐标轴和，然后确定其坐标和来确定的，即和（参见图13）。另外，正如我们在上一章中所看到的，点也可以通过“向量” 来确定，向量的概念不仅包括一个确定的方向，还有一个确定的长度。从抽象的数学角度来看，任意选择原点的概念可能显得人造且笨拙，类似地，任意绘制的坐标轴和也是如此。但在将数学应用于宇宙事件时，我们通过直接简单的方式象征性地表达了我们感官所提供的关于世界的最基本的观点。我们每个人都会将我们对事物的感性认知参照一个我们称之为“这里”的原点；我们在空间中的特定位置，围绕这个位置我们将整个宇宙聚集在一起，是我们身体存在的本质事实。我们可以想象有些存在能够以平等的眼光观察所有空间中的现象，不偏向任何一个部分。而在我们这里情况不同，脚下的猫比位于霍恩角的地震，或比银河系中一个世界的毁灭更能引起我们的关注。确实，在与他人共同积累我们的知识时，我们不得不放弃一些我们个人“这里”的严格自我主义。我们用“几乎在这里”来代替“在这里”；因此，我们从最近城市的市政厅或国家的首都开始测量英里。在测量地球时，科学家们将原点设在地球的中心；天文学家甚至上升到极端的利他主义，将原点放在太阳内部。但无论这个最后的原点多么遥远，甚至如果我们进一步选择一个在更近的固定星系中的便利点，然而，与空间的无尽广袤相比，仍然可以说，我们探索宇宙的初步步骤是确定一个“近这里”的原点。

Again the relation of the co-ordinates and (i.e and ) to the vector is an instance of the famous parallelogram law, as can easily be seen (cf.Fig.8) by completing the parallelogram . The idea of the 'vector' , that is, of a directed magnitude, is the root-idea of physical science. Any moving body has a certain magnitude of velocity in a certain direction, that is to say, its velocity is a directed magnitude and has a definite direction. Thus, when in analytical geometry the ideas of the 'origin',of 'co-ordinates', and of 'vectors' are introduced, we are studying the abstract conceptions which correspond to the fundamental facts of the physical world.

再者，坐标和（即和）与向量的关系是著名的平行四边形法则的一个例子，正如通过完成平行四边形（参见图8）可以很容易看出。‘向量’ 的概念，即带方向的量，是物理科学的根本概念。任何运动物体都有一个在特定方向上的速度大小，换句话说，它的速度是一个带方向的量，并且有一个确定的方向。因此，当在解析几何中引入‘原点’、‘坐标’和‘向量’的概念时，我们实际上是在研究与物理世界基本事实相对应的抽象概念。